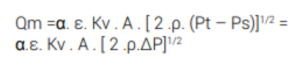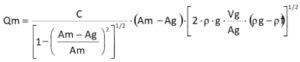La portata è la variabile di processo che è sinonimo di energia utilizzata nei vari impianti per realizzare processi chimici, temici, siderurgici ecc. oppure di energia prodotta e fornita negli impianti energetici e oil&gas in particolare, la cui corretta e precisa misura, è richiesta nelle prime applicazioni per determinare i consumi e rendimenti degli impianti e, nelle seconde applicazioni, per determinare la produzione e fornitura degli impianti a scopo di valutare l’entità delle transazioni commerciali anche a fini fiscali.

Misuratori a tubo di Pitot
Il principio di funzionamento di questi misuratori si basa sulla legge di Bernoulli. Sono dei misuratori costituiti da una sonda che presenta due prese di pressione: una di impatto investita dal fluido in misura (presa di pressione dinamica o totale – Pt), e l’altra di stagnazione posizionata ortogonalmente al flusso del fluido (presa di pressione statica – Ps). L’equazione funzionale è la seguente:

dove: α = coeffciente di portata: vale tipicamente 1,0 per i tubi di Pitot classici (ISO 3966)
. ε= coeffciente di comprimibilità: vale 1 per i liquidi e tipicamente (1- 0,2.∆P/P) per gas e vapori
Kv = coeffciente di velocità che è funzione del Numero di Reynolds della corrente fluida: vale 1, per installazione al punto di velocità media del fluido in misura (ISO 7145): a 0,146 D e a 0,121 D rispettivamente in moto laminare e turbolento (D = diam. tubaz.), oppure a 0,125 D (a 1/8 D) a prescindere della conoscenza del regime del moto fluido.

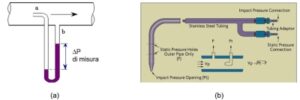
Principio di funzionamento del Pitot Classico (a) Pressione differenziale di misura ∆P tra la p.d.p. totale Pt “a” e la p.d.p. statica Ps “b” (b) Vista di un Pitot normalizzato ISO 3966 con la p.d.p. Pt “Impact Pressure” e la Ps “Static Pressure”

Esistono anche dei Pitot Speciali diritti adatti per misure al centro della tubazione e pertanto da compensare per il regime del moto fluido. Ne esistono anche per misure multi puntuali (min 2 punti per piccoli diametri e anche > di 10 per grandi diametri) lungo tutto il diametro della tubazione e pertanto che rilevano la velocità media secondo il metodo della traversa (ISO 3966) e quindi compensati per il tipo di regime del fluido. Questi ultimi possono avere una sola presa di pressione statica sul retro, oppure possono avere le prese di pressione statiche di uscita simmetriche a quelle dinamiche di ingesso e quindi li rende adatti anche per misure di portata bidirezionali.

Misuratori ad area variabile
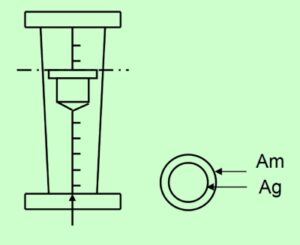
Il principio di funzionamento di questi altri misuratori si basa anch’esso sulla legge di Bernoulli. Sono dei misuratori che mantenendo costante la pressione differenziale tra monte e valle dell’elemento sensibile (galleggiante), al variare della portata, variano l’area di passaggio del fluido nel tubo conico di misura (e perciò chiamati ad area variabile) e che provoca una variazione di posizione (altezza) del galleggiante, che viene indicata localmente e/o trasmessa a distanza, come:

dove, g è l’accelerazione di gravità, Ag Vg e ρg sono rispettivamente l’area, il volume e la densità del galleggiante, ρf è la densità del fluido e Am l’area del misuratore all’altezza di misura essendo il tubo conico.

Questi misuratori sono standardizzati dalla Norma Tedesca VDE/VDI 3313 che prevede 5 classi di precisione che vanno dal’1% al 6% del fondo scala.

Misuratori magnetici
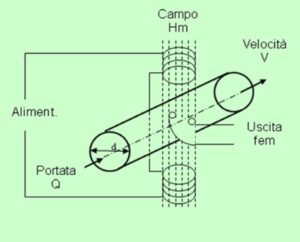
Il principio di funzionamento di questi misuratori si basa sulla legge di Faraday dell’induzione magnetica che stabilisce che un conduttore (in questo caso il liquido conduttore stesso) immerso in un campo magnetico produce ai suoi estremi una forza elettro motrice (f.e.m.) proporzionale alla velocità con cui il conduttore taglia le linee di flusso del campo magnetico, secondo la seguente relazione: Qm = A . V . ρ dove la velocità V è ricavabile dalla forza elettro motrice Em generata per la legge di Faraday: V = Em / Km · Hm · d dove Km è il fattore di proporzionalità del misuratore e Hm è il campo magnetico e d è il diametro.

Questi misuratori sono adatti per soli liquidi conduttori aventi una conducibilità elettrica minima di 5 µS/cm (o anche di 0,05 µS/cm nel caso di misuratori a elevata sensibilità con accoppiamento capacitivo anziché resistivo) e quindi sono ideali per tutte le sostanze acquose con un elevato campo di lavoro di 20:1 non risentendo della viscosità del liquido, sono adatti a lavorare in regime laminare e/o turbolento. 

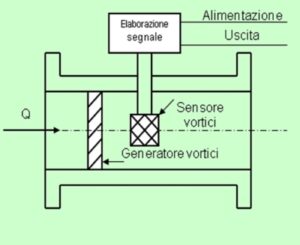
Misuratori a vortici
Il principio di funzionamento di questi misuratori si basa sulla legge di Karman che studiò e codificò la formazione di vortici dei fluidi in moto, scoperti mezzo millennio prima da Leonardo da Vinci. I vortici sono provocati da un opportuno corpo sagomato di forma trapezoidale installato nel centro della tubazione di efflusso in regime turbolento e la cui frequenza è lineare con la velocità del fluido, per cui la portata è data dalla seguente relazione: Qm = A · V · ρ = A · Kmf · f · ρ essendo la velocità di efflusso del fluido V legata alla frequenza di formazione dei vortici f, attraverso la costante del misuratore a vortici Kmf: V = Kmf · f.

La frequenza di formazione dei vortici f, è funzione della velocità del fluido e della geometria del corpo generatore dei vortici, secondo la relazione definita successivamente da Strouhal: f = St · V/d dove St è il Numero di Strouhal, e d è il diametro o lo spessore del corpo generatore dei vortici. Sono dei misuratori di buona precisione adatti per liquidi, gas e vapori.

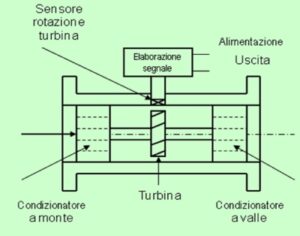
Misuratori a turbina
Sono dei misuratori a elica, a mulinello, ecc. composti da una girante leggera che rileva la velocità di una corrente fluida (liquido o gas) e la trasforma in moto rotatorio, la cui velocità è funzione della portata fluente. L’equazione funzionale è la seguente:
– in volume: Qv = Kmt · nmt
– in massa: Qm = Kmt · nmt · ρ
dove Kmt è la costante di taratura della turbina e nmt è il suo numero di giri.

Sono dei misuratori molto precisi per liquidi e gas e quindi impiegati in transazioni commerciali e fiscali, nel qual caso le Norme Americane API prevedono:
– Un filtro a monte della turbina
– Un raddrizzatore di flusso a monte della turbina
– 10 D di tratti rettilinei a monte della turbina
– 5 D di tratti rettilinei a valle della turbina
Mentre le Norme Internazionali ISO 9951 prescrivono le seguenti errori max di misura:
• ± 1 % tra Q max e 0,2 Q max
± 2 % tra Q min e 0,2 Q max